

Apart from that, a triangle also has 3 vertices. All sides and angles in a triangle have different sizes. Triangles based on the length of their sides are divided into several types. equilateral triangle, isosceles triangle and any triangle.
Meanwhile, based on the angles, triangles are also divided into 3: right triangles, obtuse triangles and acute triangles. To calculate triangles, there are two formulas. Formula for the area of a triangle and formula for the perimeter of a triangle.
Types of Triangles
1. Types of triangles based on side length
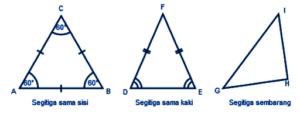
a. Equilateral triangle
An equilateral triangle is a triangle that has the same side lengths. All three sides are the same length. Apart from the same side lengths, an equilateral triangle also has three equal angles.
Triangle ABC is an example of an equilateral triangle. It can be seen that the three side lengths and angles are the same.
AB = BC = AC, this means that Angle A = angle B = angle C
b. Isosceles triangle
An isosceles triangle is a triangle in which 2 of the 3 sides have the same length. Unlike an equilateral triangle, an isosceles triangle only has two equal sides, namely the two legs.
An isosceles triangle also has a pair of angles that are the same size. An example is triangle DEF . The only sides FD and FE have the same length. Meanwhile, the DE side has a different length.
c. Any triangle
This triangle is different from the other two triangles. An arbitrary triangle is a triangle whose sides all have different lengths.
An arbitrary triangle is a triangle whose three sides have different lengths. For example, in the GIH triangle. It can be seen that none of the three sides of the GIH triangle are the same.
The book Mathematical Thinking: Mathematics for All aims to introduce new, more universal concepts for teaching mathematics to students in schools, from elementary school to middle school.
As a replacement for the method of introducing formulas and their derivation to female students, this book offers a method that introduces simple techniques to be able to solve problems using this method. It is hoped that teachers can make students understand the solving process and be able to solve the problems given independently.
2. Types of triangles based on angle sizes


a. Acute triangle
An acute triangle is a triangle whose angles are all less than 90°.
b. Right triangle
A right triangle is a triangle whose one angle is 90°.
c. Obtuse triangle
An obtuse triangle is a triangle in which one of the three angles has a greater degree. More than 90°.
This book is a mathematics book that contains basic mathematical information. This book is suitable as a reference and reference for students who want to learn about mathematics.
Example Questions and Triangle Formulas
1. Equilateral Triangle Formula
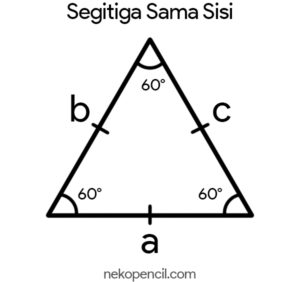

Example Question 1
Known: There is a triangle ABC, the triangle is an equilateral triangle. It is 20 cm high and has a base length of 40 cm.
Asked: What is the area and perimeter of the triangle?
Answer:
- Area of triangle ABC
L = ½ × a × t
a (base) = 40 cm
t (height) = 20 cm
So the area is:
L = ½ X 40 X 20 = 400 cm
- Perimeter of triangle ABC
K = s + s + s
S = side (the sides of an equilateral triangle have the same length)
Then the circumference is equal to:
K = 40 + 40 + 40 = 120 cm
Example Question 2
It is known that a triangle has a base of 5 cm and a height of 6 cm.
Asked: what is the area of the triangle?
Answer:
Formula:
½. base height
L = ½ x 5 x 6
= 15 cm
Example Question 3
It is known that an equilateral triangle has a side length of 5 cm.
Asked: what is the perimeter of the triangle?
Answer:
Formula
K = a + b + c
K = 5 + 5 + 5
K = 15 cm
Example Question 4
If there is an equilateral triangle with a base length of 20 cm and a height of 10 cm.
What is the area and perimeter of the triangle?
Answer:
L = ½ . a. t
= ½ x 20 x 10
= 100 cm²
K = s + s + s
= 20 + 20 + 20
= 60 cm
2. Isosceles Triangle Formula
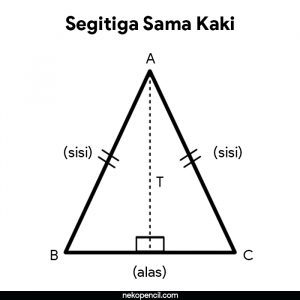
Example Question 1
Known: There is a triangle CDE, the triangle is an isosceles triangle. It is 10 cm high and has a base length of 20 cm. Both sides are 60 cm long
Asked: What is the area and perimeter of the triangle?
Answer:
- Area of triangle CDE
L = ½ × a × t
a (base) = 20 cm
t (height) = 10 cm
So the area is:
L = ½ X 20 X 10 = 100 cm
- Perimeter of triangle CDE
K = s + s + s
S = side
So the circumference is:
K = 20 + 60 + 60 = 140 cm
Example Question 2
It is known that an isosceles triangle has equal sides, namely 5 cm and a base of 4 cm.
Calculate the perimeter of the isosceles triangle?
Answer:
K = 2a + b
= 2 (5) + 4
= 10 + 4
= 14 cm
Example Question 3
It is known that an isosceles triangle has sides of the same length, namely 5 cm. If there are unequal sides the length is 6 cm and the height is 4 cm.
Asked: what is the perimeter and area of the triangle?
Answer:
K = s + s + s
= 5 cm + 5 cm + 6 cm
= 16 cm
L = ½ . a. t
= ½ x 6 cm x 4 cm
= 12 cm²
Example Question 4
If there is an isosceles triangle that has a length at the base of 10 cm and a height of 12 cm.
Determine what is the area of the triangle?
Answer:
Formula
L = ½ . a. t
= ½ . 10 . 12
= 60 cm²
3. Any Triangle Formula
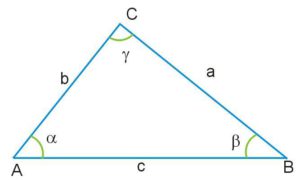
Example Question 1
Known: There is a triangle FGH, the triangle is an isosceles triangle. It is 15 cm high and has a base length of 20 cm. The sides are 17 cm and 25 cm long.
Asked: What is the area and perimeter of the triangle?
Answer:
- Area of triangle CDE
L = ½ × a × t
a (base) = 20 cm
t (height) = 15 cm
So the area is:
L = ½ X 20 X 15 = 150 cm
- Perimeter of triangle CDE
K = s + s + s
S = side
So the circumference is:
K = 20 + 17 + 25 = 62 cm
Example Question 2
It is known that any triangle has a semiperimeter value, namely 20 cm. The length of side a= 15 cm, b= 19 cm, and c= 13 cm.
Determine the area of the triangle!
Answer:
L= √(s(sa)(sb)(sc)
L= √(20(20-15)(20-19)(20-13)
L= √20.5.1.7
L= √700
L= 20√7 cm2
Example Question 3
If there is an arbitrary triangle that has a semiperimeter value of 20 cm and lengths on sides a= 15 cm, b= 12 cm, and c= 18 cm.
Calculate the area of any triangle!
Answer:
L= √(s(sa)(sb)(sc)
L= √(20(20-15)(20-12)(20-18)
L= √20.5.8.2
L= √1600
L= 20√4 cm2
That is the formula and example of a problem for a flat triangular shape. Find other interesting things at www.gramedia.com. Gramedia as #FriendsWithoutBatas will always provide recommendations for the best articles and books for Grameds.